Les résistances
Quelques définitions
Comme son nom l'indique une résistance oppose une résistance au passage du courant. À ce sujet, la loi la plus connue en électronique est sans doute la loi d'Ohm :
U=R⋅I
- U est la différence de potentiel aux bornes de la résistance, en Volt (symbole : V)
- R est la valeur de la résistance, en Ohm (symbole : Ω)
- I est le courant qui traverse la résistance, en Ampère (symbole : A)
Sur les schémas, la résistance est représentée par le symbole suivant (à gauche, le symbole européen pour une résistance de 100Ω ; à droite, le symbole américain pour une résistance de 1kΩ, soit 1000Ω) :
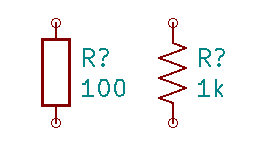
L'unité n'est pas toujours spécifiée, mais ce sont toujours des Ohm. Seul les multiples, voir des sous-multiples, sont précisés à côté de la valeur.
On mesure la valeur d'une résistance avec un Ohmmètre. D'ailleurs, l'Ohmmètre est en fait un Voltmètre mais qui utilise la loi d'Ohm. En effet, c'est généralement un appareil qui va faire circuler un courant constant connu dans la résistance à mesurer, il mesure alors la tension (d'où le Voltmètre) aux bornes de la résistances. On connait I, on mesure V, on en déduit R. CQFD.
Qu'est-ce qui caractérise une résistance ?
Sa résistance
Une résistance est d'abord caractérisée par sa valeur, en Ohm. C'est sans doute la caractéristique la plus importante, mais ce n'est pas la seule.
Si on réécrit la loi d'Ohm décrite ci-dessus, on peut aussi écrire :
R=U/I ou encore I=U/R
Mais toutes les valeurs de résistances ne sont pas disponibles. Par exemple vous ne trouverez pas une résistance de 712Ω.
En fait il existe des « séries » de résistances, la plus classique est la E24 qui comme son nom l'indique contient 24 valeurs différentes.
La série E24 se compose des valeurs suivantes : 100, 110, 120, 130, 150, 160, 180, 200, 220, 240, 270, 300, 330, 360, 390, 430, 470, 510, 560, 620, 680, 750, 820, 910
Mais alors il n'y a pas de résistance de moins de 100Ω ou de plus de 910Ω ? Bien sûr que si ! On va retrouver les mêmes valeurs dans chaque décade. Une décade va par exemple de 1 à 10, la suivante de 10 à 100, la décade suivante de 100 à 1000, etc. En gros la décade c'est l'endroit où on place la virgule ou encore le nombre de 0. Cela veut donc dire qu'on peut multiplier (ou diviser) toutes ces valeurs par des multiples de 10... les fameuses décades. ![]()
Donc avec l'exemple précédent, la valeur la plus proche de 712Ω dans la série E24, est 680Ω.
Si on prend la valeur de 680Ω, on peut la trouver dans chaque décade comme par exemple : 6,8Ω, 68Ω, 6,8kΩ, 68kΩ, 680kΩ, etc.
On a parlé de la série E24, mais il existe aussi d'autres séries assez utilisées comme la E48 ou encore E96 qui ont donc chacune 48 et 96 valeurs respectivement.
La série E48 se compose des valeurs suivantes : 100, 105, 110, 115, 121, 127, 133, 140, 147, 154, 162, 169, 178, 187, 196, 205, 215, 226, 237, 249, 261, 274, 287, 301, 316, 332, 348, 365, 383, 402, 422, 442, 464, 487, 511, 536, 562, 590, 619, 649, 681, 715, 750, 787, 825, 866, 909, 953.
La série E96 se compose des valeurs suivantes : 100, 102, 105, 107, 110, 113, 115, 118, 121, 124, 127, 130, 133, 137, 140, 143, 147, 150, 154, 158, 162, 165, 169, 174, 178, 182, 187, 191, 196, 200, 205, 210, 215, 221, 226, 232, 237, 243, 249, 255, 261, 267, 274, 280, 287, 294, 301, 309, 316, 324, 332, 340, 348, 357, 365, 374, 383, 392, 402, 412, 422, 432, 442, 453, 464, 475, 487, 499, 511, 523, 536, 549, 562, 576, 590, 604, 619, 634, 649, 665, 681, 698, 715, 732, 750, 768, 787, 806, 825, 845, 866, 887, 909, 931, 953, 976.
On peut facilement trouver un tableau de l'ensemble des valeurs des séries E3, E6, E12, E24, E48, E96 et E192.
Plus loin dans cet article est expliqué comment lire la valeur des résistances et en particulier décrypter code couleur.
Sa puissance
La deuxième caractéristique qui doit venir à l'esprit, est généralement la puissance, exprimée en Watt (symbole : W). Celle-ci indique la puissance maximale que la résistance est capable de dissiper. La puissance classique pour les résistances traversantes est d'¼W, soit 250mW ou encore 0,25W. Mais on trouve des petites résistances (CMS ou traversantes) de 0,125W, ou encore des résistances d'½W, 1W, 2W voir même 100W ou plus. Si vous avez un convecteur électrique de 2000W, c'est en fait une résistance de puissance de 2000W ![]()
La puissance dissipée par une résistance se calcule avec la formule suivante :
P=U⋅I
- P est la puissance dissipée, en Watt (symbole : W)
- U est la différence de potentiel aux bornes de la résistance, en Volt (symbole : V)
- I est le courant qui traverse la résistance, en Ampère (symbole : A)
Note : cette formule est générale et ne s'applique pas qu'aux résistances.
Si on combine avec la loi d'Ohm, on peut aussi écrite que:
P=R⋅I² ou encore P=U²/R
On voit que la puissance dissipée croit selon le carré de l'intensité du courant qui traverse la résistance. Dans une résistance, la puissance ne se dissipe que sous forme de chaleur. C'est pour ça que dissiper une puissance de 4W dans une résistance capable de dissiper ½W fini généralement mal...
Sa tolérance
Avec la valeur de la résistance, on associe souvent aussi la tolérance, en %. Les résistances classiques ont une tolérance de 5%, c'est à dire que la valeur réelle peut être ±5% par rapport à la valeur indiquée. Par exemple, une résistance de 1kΩ 5% peut être mesurée à l'Ohmmètre avec une valeur entre 950Ω et 1050Ω (si on ne tient pas compte de la précision de l'Ohmmètre et qu'on suppose qu'il est calibré, car lui aussi a une tolérance).
Les résistances à 1% sont devenues assez courantes maintenant, celles de 10% ou même plus ont disparues. On trouve aussi des résistance de grande précision, comme par exemple à 0,01%. Le prix de ce genre de résistance est très élevé. Les résistances de 5% ou 1% conviennent à la quasi totalité des besoins.
Les valeurs des résistances à 5% utilisent la série E24, celles à 1% généralement la série E24 ou E96.
Sa tension maximale
On a souvent tendance à l'oublier car pour la plupart des montages cette caractéristique n'est pas du tout un problème, mais chaque résistance a une tension maximale, aussi appelée tension critique, exprimée en Volt.
Cette valeur est souvent de l'ordre de 200V-300V. C'est pour ça que pour le bidouilleur classique qui ne joue pas avec le secteur, n'a que faire de cette caractéristique. Mais dès qu'on joue avec le secteur ou de la haute tension, ce paramètre est à prendre en compte.
Son coefficient de température
La valeur de la résistance peut varier plus ou moins avec la température. Là aussi ce paramètre est souvent négligeable pour le bidouilleur classique. Ce coefficient, s'exprime souvent en ppm/K (ou plus rarement en ppm/°C). Cela signifie partie par million par Kelvin ou par degrés Celcius. Sachant que l'écart entre 1K et 1°C est identique, ces 2 unités sont totalement identiques.
1ppm/K = 1ppm/°C
Mais à quoi cela correspond ? C'est un peut comme des pourcents % qui correspondent à des parties pour cent unités, sauf que là ce sont des parties pour 1 million d'unités. Donc vu que les % revient à diviser par 100, pour les ppm il faut diviser par un million. Enfin, même si les parties dont il est question ici, sont les Ohms, les ppm n'ont en soit pas d'unité et peuvent s'appliquer à tout ce qu'on veut, exactement comme les %.
Par exemple, pour une résistance ayant un coefficient de température de 250ppm/K, si sa température augmente de 100°C, on va avoir une variation de 100*250ppm, soit 25000ppm. On a vu que le fait qu'on parle de K ou °C ne changeait rien ici. 25000ppm = 25000/1000000 = 25/1000 = 2,5/100 = 2,5%. Donc une telle résistance qui a été mesurée à 105Ω à 25°C, si la température varie de ±100°C la valeur de cette résistance pourra changer de ±2,5%, soit ±2,625Ω. On pourra donc mesurer cette même résistance entre 102,4Ω et 107,6Ω.
Certaines résistances particulières cherchent à avoir un coefficient de température constant et précis, on pourra alors les utiliser pour mesurer la température par exemple. Il y en a ou la valeur diminue avec la chaleur, on parle alors de NTC ; d'autres au contraire, leur valeur augmente avec la température, ce sont les PTC.
Autres caractéristiques
Il existe plusieurs autres caractéristiques, comme par exemple son facteur de forme c'est à dire si c'est un composant à monter en surface, à trou traversant, à visser sur un chassis, de quelle taille, etc. Mais il y a aussi est-ce qu'elle est garantie de ne pas prendre feu (flameproof) lorsqu'on dépasse sa puissance maximale, etc. Il y a aussi la constitution de la résistance, comme par exemple au carbone ou fil métallique bobiné. Cela peut avoir de l'importance car le fil bobiné joue aussi le rôle de... bobine, donc d'inductance, ce qui peut poser des problèmes dans certains cas.
Maintenant, certains se demandent aussi la signification de la couleur du corps de la résistance... À rien ! En fait, cela dépend de la marque mais rien n'est normalisé et vu qu'on a aucune idée de la marque ou du modèle de la résistance en la regardant, impossible de savoir.
Le code couleur des résistances et les notations sur les CMS
La valeur des résistances est indiquée dessus :
- Soit en clair pour les grosses résistances de puissances,
- Soit en chiffres sur les CMS. Le R éventuel remplace le point, par exemple 4R0 veut dire 4Ω. S'il n'y a que des chiffres, le dernier correspond au nombre de 0. Par exemple 100 ne veut pas dire 100Ω mais 10 suivi de 0 zéro, donc 10Ω. 100Ω serait écrit 101 : 10 suivi d'1 zéro.
- Les résistances à trou traversant utilisent généralement les anneaux de couleur. On peut trouver un convertisseur sur le site de Digi-Key
Trouver les bandes de couleurs correspondant à la valeur
Il est quand même bien de connaître le code couleur. Plus il y a de bandes, plus il y a de chiffres et donc plus on est précis. Les résistances classiques ont 4 ou 5 bandes généralement. Jusqu'à 5 bandes, la dernière indique la précision et l'avant-dernière le facteur multiplicateur.
| Couleur | Bande 1 | Bande 2 | Bande 3 | Avant-dernière | Dernière bande |
| Noir | 0 | 0 | 0 | ×100 (×1) | |
| Marron | 1 | 1 | 1 | ×101 (×10) | ±1% |
| Rouge | 2 | 2 | 2 | ×102 (×100) | ±2% |
| Orange | 3 | 3 | 3 | ×103 (×1k) | |
| Jaune | 4 | 4 | 4 | ×104 (×10k) | |
| Vert | 5 | 5 | 5 | ×105 (×100k) | ±0,5% |
| Bleu | 6 | 6 | 6 | ×106 (×1M) | ±0,25% |
| Violet | 7 | 7 | 7 | ×107 (×10M) | ±0,1% |
| Gris | 8 | 8 | 8 | ×108 (×100M) | ±0,05% |
| Blanc | 9 | 9 | 9 | ×109 (×1G) | |
| Or | ×10-1 (÷10) | ±5% | |||
| Argent | ×10-2 (÷100) | ±10% |
Selon le nombre de bande sur la résistance, il n'y aura entre 1 et 3 chiffres, les colonnes «bande 2 » et « bande 3 » pourront alors éventuellement être ignorées.
Exemples :
| Valeur | 4 bandes (≡2 chiffres) | 5 bandes (≡3 chiffres) | CMS (2+1 chiffres) | CMS (3+1 chiffres) |
| 680Ω | =68×101 | =680×100 | 681 | 6800 |
| 1kΩ | =10×103 | =100×102 | 103 | 1002 |
| 4,7kΩ | =47×102 | =470×101 | 472 | 4701 |
| 10kΩ | =10×104 | =100×103 | 104 | 1003 |
| 71,5kΩ | impossible (>2 chiffres) | =715×102 | impossible (>2 chiffres) | 7152 |
On note que la précision ne figure pas sur les résistances CMS. De même, si elles sont trop petites, il n'y aura aucune inscription dessus.
Trouver la valeur correspondante aux bandes de couleur
Vert-Marron-Noir-Rouge-Marron ?
Nous avons moins de 6 bandes, donc :
- la dernière est pour la précision: marron correspond à ±1%
- l'avant-dernières correspond au facteur multiplicateur, ou autrement dit à la puissance de 10 : rouge correspond à ×102
- Les 2 bandes restantes au début sont donc les 3 chiffres significatifs:
- Vert correspond à 5
- Marron correspond à 1
- Noir correspond à 0
On remet tout dans l'ordre et ça nous donne : 5 1 0 ×102 ±1% = 5 1 0 00 = 51000 = 51kΩ ±1%
Comment trouver la résistance qu'il nous faut ?
La formule la plus utilisée en électronique est la loi d'Ohm donnée au début de cet article. Pour trouver la valeur de la résistance, on va souvent utiliser les 2 formules suivantes: R=U/I et P=U²/R.
Supposons que nous devons allumer une LED RGB (ou RVB en français, Rouge, Vert, Bleu) à anode commune depuis une alimentation 5V. Une LED RGB est à traiter comme si nous avions 3 LED, une verte, une rouge et une bleue dans le même boîtier. La couleur de chaque LED est important car comme on peut le voir dans le datasheet, les caractéristiques ne sont pas identiques.
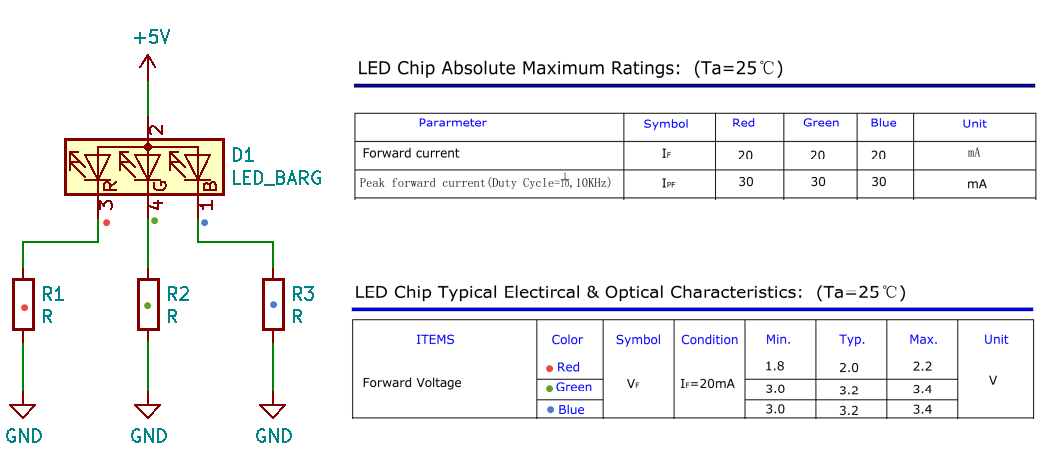
Calculons les valeurs des LED R1, R2 et R3 nécessaires en fonction des données du datasheet de cette LED RGB. On voit que pour chaque LED, le courant maximal dans le sens passant (IF) est de 20mA. Si on note IR, IG, IB le courant pour chaque LED, cela veut donc dire que IR=IG=IB=IF=0,02A.
Pour calculer R, il nous faut U et I. Nous avons donc déjà I (0,02A). Il reste à déterminer U pour chaque LED.
Pour calculer U1 qui est la différence de potentiel aux bornes de R1, la résistance qui va réguler le courant dans la LED rouge, le datasheet indique que si un courant de 20mA traverse la LED rouge, on aura une tension aux bornes de la LED comprise entre 1,8V et 2,2V. Prenons la valeur typique, soit 2V. Sachant que nous avons 5V entre la masse (GND) et l'alimentation, cela veut dire que nous devons avoir 3V (5V-2V) aux bornes de R1. Nous avons donc tout pour calculer R1: R1=U1/IR=3V/0,02A=150Ω
De la même façon, la tension aux bornes de la LED verte est comprise entre 3V et 3,4V pour un courant de 20mA. Prenons 3,2V. On a donc U2=5V-3,2V=1,8V. Donc R2=U2/IG=1,8V/0,02A=90Ω
En faisant de même avec la LED bleue, on a la même chose que pour la LED verte, donc R3=90Ω
On voit que la valeur des résistances sont différentes selon la couleur des LED. Maintenant, regardons si ces valeurs existent dans la série E24. R1 existe, il y a bien 150Ω. Pour R2 et R3, il n'y a pas 90 dans la liste. Attention, on peut se dire que la valeur la plus proche est la première, 100, mais non. Je rappelle que les valeurs sont par décade. Or il y a 910 dans la liste, qui sur une autre décade (ici, si on enlève un zéro) est 91. Donc la résistance la plus proches est 91Ω.
Est-ce grave de ne pas avoir exactement 90Ω ? Déjà, on sait que d'après la tolérance, une résistance de 91Ω à 5% a une valeur comprise entre 90,55Ω et 91,45Ω. Calculons le courant dans la LED pour une résistance de 91Ω. Le courant dans la LED sera le même que celui dans la résistance, or pour la résistance, IR=U2/R2=1,8V/91Ω=19,8mA. On voit donc qu'utiliser une diode de 91Ω à la place des 90Ω calculés ne pose aucun problème. Cela montre aussi que dans la plupart des cas, cela ne sert à rien de choisir des résistances avec une faible tolérance (et donc plus coûteuse).
Dans notre exemple, nous utiliserons donc les résistances suivantes : R1=150Ω, R2=R3=91Ω. Il est possible d'utiliser des valeurs plus grande si on souhaite faire passer moins de courant dans les LED. Je vous laisse calculer les valeurs qu'il faudrait pour ne faire passer que 10mA au lieu des 20mA.
Astuce : on divise le courant par 2, or R=U/I, du coup vous pouvez deviner facilement les valeurs des résistances à utiliser sans refaire tout le calcul.
Astuce 2 (pour ceux qui n'ont pas trouvé) : diviser une valeur par une valeur qui est elle-même divisée par 2, revient à multiplier 2 le résultat de la division initiale.
Par contre, il ne faut pas utiliser des valeurs plus petite que celles calculées ici pour 20mA car on aurait un courant plus grand, qui dépasseraient les valeurs spécifiées par le constructeur et qui vont écourter la durée de vie des LED, parfois énormément... R.I.P.
Maintenant que nous avons les valeurs, comment les trouver sur les composants à portée de main ?
Dans le cas présent, nous n'allons pas utiliser de grosse résistance de puissance.
- Si nous voulons utiliser des résistances CMS (composant monté en surface), on doit avoir ces inscriptions sur les résistances :
- R1 : 150Ω c'est un 15 suivi de 1 zéro, donc 151
- Pour R2 et R3: 91Ω, c'est 91 suivi de 0 zéro, donc 910. Et oui, on peut penser qu'une résistance sur laquelle est inscrit 910 est plus grande qu'une où il est inscrit 151... Et bien non ! Mais maintenant vous savez pourquoi.

- Si nous voulons utiliser des résistances classiques (à trou traversant), il faut utiliser le code des couleurs. Si on utilise par exemple celui de Digi-Key donné juste au dessus, on a :
- R1 : 150Ω, c'est 15 avec un multiplicateur x10, donc marron-vert-marron suivi d'un anneau or pour une précision à ±5%. D'ailleurs, on peut voir que marron vaut 1 et le vert vaut 5. Du coup le code couleur nous donne 151, comme sur la résistance CMS

- R2 et R3 : 91Ω c'est 91 x1, donc blanc-marron-noir suivi d'un anneau or. Là encore, le code couleur nous donne 910, exactement ce qu'on a sur la diode CMS.
- R1 : 150Ω, c'est 15 avec un multiplicateur x10, donc marron-vert-marron suivi d'un anneau or pour une précision à ±5%. D'ailleurs, on peut voir que marron vaut 1 et le vert vaut 5. Du coup le code couleur nous donne 151, comme sur la résistance CMS
Étude d'un datasheet
Prenons par exemple le datasheet des résistances SFR16S, SFR25, SFR25H de chez Vishay :
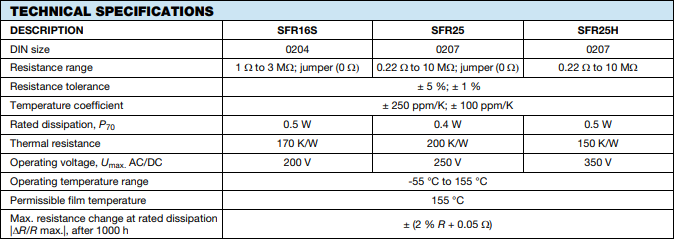
Si on regarde les SFR16S par exemple, on voit que :
- La puissance maximale est de 500mW
- La tension à ses bornes ne doit pas dépasser 200V.
- Les valeurs disponibles sont entre 1Ω et 3MΩ, ainsi qu'une résistance de 0Ω.
- Il existe plusieurs tolérances et le coefficients de température
Sur la page suivante du datasheet on peut voir quelles sont les séries de valeurs disponibles :
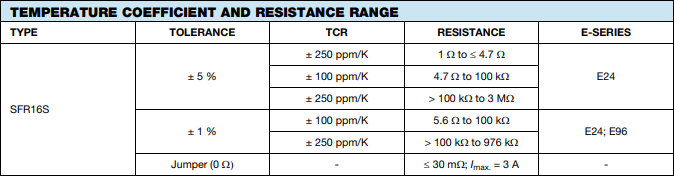
Si on choisi des résistances SFR16S 1%, on voit que les valeurs disponibles sont toutes les valeurs des séries E24 et E96 allant de 5,6Ω à 976kΩ. Le coefficient de température est différent selon la valeur de la résistance.
Exemple concret
Je n'ai pas parlé de la résistance thermique, mais 170K/W, cela signifie que la température de la résistance va augmenter de 170°C par Watt dissipé. Par exemple, supposons qu'on a une résistance de 2kΩ et qu'on aura à ses bornes 100V. On peut penser que c'est bon car elle est conçue pour tenir jusqu'à 200V et 2kΩ fait bien partie de la série E24. La loi d'Ohm nous dit aussi que I=U/R, donc I=100V/2000Ω = 0,05A = 50mA. P=U⋅I=100V⋅0,05A=5W ce qui est largement supérieur à ce qu'est capable de dissiper cette résistance (0,5W), elle risque de prendre feu ! Pour le fun, calculons son élévation de température. Le datasheet nous donne 170K/W. Donc 5W*170K/W=850°C ! Elle est donnée pour être utilisée jusqu'à 155°C, autant dire qu'elle est partie au paradis des résistances. ![]() Pour être honnête, la température calculée peut être fausse car on est bien au-delà des spécifications du datasheet. Ce qui est sûr c'est que cette résistance ne s'en remettra pas.
Pour être honnête, la température calculée peut être fausse car on est bien au-delà des spécifications du datasheet. Ce qui est sûr c'est que cette résistance ne s'en remettra pas.
Mais alors, comment faire ?
- Soit prendre une résistance de puissance, d'au moins 5W. Il est même préférable de garder une marge et de ne pas dépasser 70% de la puissance maximale, soit 5W*100/70 ≈ 7W
- Soit mettre plusieurs résistances en série ou en parallèle pour répartir cette puissance dissipée (qui au totale sera la même). Dans le cas présent, il faudra minimum 10 résistances (5W/0.5W), comme par exemple 10 résistance de 200Ω en série. Là aussi, il est préférable de garder une marge de sécurité. On pourrait donc utiliser 20 résistances de 100Ω en série.
- Ou encore un mix de ces 2 premières solutions, comme utiliser 2 résistances de 1kΩ 4W en série, chacune dissipera alors 2,5W, ce qui représente 63% de leur puissance maximale.
Quels sont les autres types de résistances ?
Nous avons vu les resistances fixes, mais il existe d'autres types de résistances comme par exemple :
- Les résistances variables (rhéostats, potentiomètres, trimmers)
- Les thermistances dont la valeur varie fortement avec la température (PTC, NTC)
- Les photo-resistances dont la valeur change en fonction de la lumière